Obliczanie logarytmu może wydawać się skomplikowane, ale w rzeczywistości jest to proces oparty na prostych zasadach matematycznych. Logarytm to odwrotność działania wykładniczego, co oznacza, że pozwala nam znaleźć, do jakiej potęgi musimy podnieść daną podstawę, aby uzyskać określoną liczbę. Na przykład, logarytm przy podstawie \(a\) z liczby \(b\) to taka liczba \(x\), że \(a\) podniesione do potęgi \(x\) daje \(b\).
W tej artykule przedstawimy proste metody obliczania logarytmu oraz praktyczne przykłady, które pomogą zrozumieć ten temat. Dowiesz się, jak obliczać logarytmy przy podstawie 10 oraz logarytmy naturalne, a także poznasz ich zastosowania w różnych dziedzinach, takich jak finanse czy nauki przyrodnicze.
Najistotniejsze informacje:- Logarytm to odwrotność działania wykładniczego, co ułatwia obliczenia.
- Logarytm przy podstawie \(a\) z liczby \(b\) określa, do jakiej potęgi należy podnieść \(a\), aby otrzymać \(b\).
- Obliczanie logarytmu przy podstawie 10 jest jedną z najczęściej stosowanych metod.
- Logarytmy naturalne (przy podstawie \(e\)) mają szerokie zastosowanie w matematyce i naukach przyrodniczych.
- Logarytmy są używane w finansach do analizy wzrostu inwestycji oraz obliczeń związanych z oprocentowaniem.
Jak obliczyć logarytm: podstawowe definicje i zasady
Logarytm to pojęcie, które może wydawać się skomplikowane, ale w rzeczywistości opiera się na prostych zasadach matematycznych. Logarytm jest odwrotnością działania wykładniczego, co oznacza, że pozwala nam określić, do jakiej potęgi musimy podnieść daną podstawę, aby uzyskać określoną liczbę. Na przykład, logarytm przy podstawie \(a\) z liczby \(b\) to taka liczba \(x\), że \(a\) podniesione do potęgi \(x\) daje \(b\).
Warto zrozumieć, że logarytmy są niezwykle użyteczne w wielu dziedzinach matematyki i nauki. Dzięki nim możemy łatwo rozwiązywać równania wykładnicze oraz analizować różnorodne zjawiska. W tej sekcji omówimy podstawowe definicje logarytmu oraz zasady, które pomogą w jego obliczaniu.
Logarytm jako odwrotność działania wykładniczego
Logarytm to narzędzie, które pozwala nam zrozumieć relację między liczbami w kontekście potęg. Jako odwrotność działania wykładniczego, logarytm odpowiada na pytanie: "Jaką potęgę musimy podnieść do danej podstawy, aby uzyskać określoną wartość?" Na przykład, jeśli mamy równanie \(2^x = 8\), to logarytm przy podstawie 2 z liczby 8 wynosi 3, ponieważ \(2^3 = 8\).
Ta odwrotna relacja jest kluczowa w wielu zastosowaniach matematycznych. Umożliwia przekształcanie skomplikowanych równań wykładniczych w prostsze formy, które można łatwiej analizować. Logarytmy są także wykorzystywane w statystyce, naukach przyrodniczych oraz finansach, gdzie pomagają w analizie danych i wzrostu wartości.
Zrozumienie podstawy logarytmu i jego znaczenie
Podstawa logarytmu jest kluczowym elementem, który definiuje, jak obliczamy logarytm. Podstawą logarytmu jest liczba, do której potęgi musimy podnieść, aby uzyskać daną wartość. Na przykład, w logarytmie przy podstawie 10, oznaczamy to jako logarytm dziesiętny, co jest powszechnie stosowane w różnych obliczeniach.
W matematyce wyróżniamy różne podstawy logarytmów, takie jak 2, 10 czy e (podstawa logarytmu naturalnego). Różne podstawy mają różne zastosowania i znaczenie w obliczeniach. Na przykład, logarytmy o podstawie 10 są często używane w naukach ścisłych i finansach, podczas gdy logarytmy naturalne (z podstawą e) są bardziej popularne w matematyce teoretycznej oraz w analizie danych.
Proste metody obliczania logarytmu: krok po kroku
Obliczanie logarytmu może być proste, jeśli zrozumiemy kilka podstawowych metod. Jedną z najczęściej stosowanych metod jest użycie kalkulatora, który ma funkcję logarytmu. Wystarczy wpisać liczbę, a następnie wybrać odpowiednią podstawę, aby uzyskać wynik. To szybki sposób na obliczenie logarytmu, szczególnie w przypadku bardziej skomplikowanych liczb.
Inną metodą jest korzystanie z tabel logarytmicznych, które zawierają wartości logarytmów dla najczęściej używanych liczb. Te tabele mogą być bardzo pomocne, gdy nie mamy dostępu do kalkulatora. Warto jednak pamiętać, że w dzisiejszych czasach większość ludzi korzysta z technologii, co czyni obliczenia bardziej dostępnymi i szybszymi.
Obliczanie logarytmu przy podstawie 10: przykład praktyczny
Obliczanie logarytmu przy podstawie 10, znane również jako logarytm dziesiętny, jest jedną z najczęściej stosowanych metod w matematyce. Aby obliczyć logarytm dziesiętny, należy znaleźć taką potęgę liczby 10, która daje daną wartość. Na przykład, logarytm dziesiętny z liczby 1000 to 3, ponieważ \(10^3 = 1000\).
W praktyce, aby obliczyć logarytm dziesiętny, można użyć kalkulatora, który ma funkcję logarytmu. Wystarczy wpisać liczbę, a kalkulator zwróci wynik. Można również korzystać z tabel logarytmicznych, które zawierają wartości logarytmów dla najczęściej używanych liczb. Poniżej znajduje się tabela porównawcza wyników obliczeń logarytmów dla różnych liczb przy podstawie 10.
| Liczba | Logarytm dziesiętny |
|---|---|
| 10 | 1 |
| 100 | 2 |
| 1000 | 3 |
| 10000 | 4 |
Jak obliczyć logarytm naturalny: zastosowanie i przykłady
Logarytm naturalny, oznaczany jako ln, jest logarytmem przy podstawie e, gdzie e to liczba około 2.71828. Obliczanie logarytmu naturalnego polega na znalezieniu potęgi liczby e, która daje daną wartość. Na przykład, logarytm naturalny z liczby e wynosi 1, ponieważ \(e^1 = e\).
Logarytmy naturalne mają szerokie zastosowanie w matematyce, naukach przyrodniczych oraz inżynierii. Używa się ich do modelowania wzrostu populacji, procesów chemicznych oraz w finansach przy obliczaniu odsetek składanych. Przykładem może być obliczenie logarytmu naturalnego z liczby 7, co daje około 1.94591. Poniżej znajduje się lista zastosowań logarytmów naturalnych w różnych dziedzinach.
- Analiza danych w statystyce i ekonomii.
- Modelowanie wzrostu populacji w biologii.
- Obliczenia w chemii dotyczące reakcji i stężeń.
Czytaj więcej: Jak otworzyć plik PDF w Wordzie i uniknąć problemów z formatowaniem
Przykłady obliczeń logarytmu w różnych kontekstach
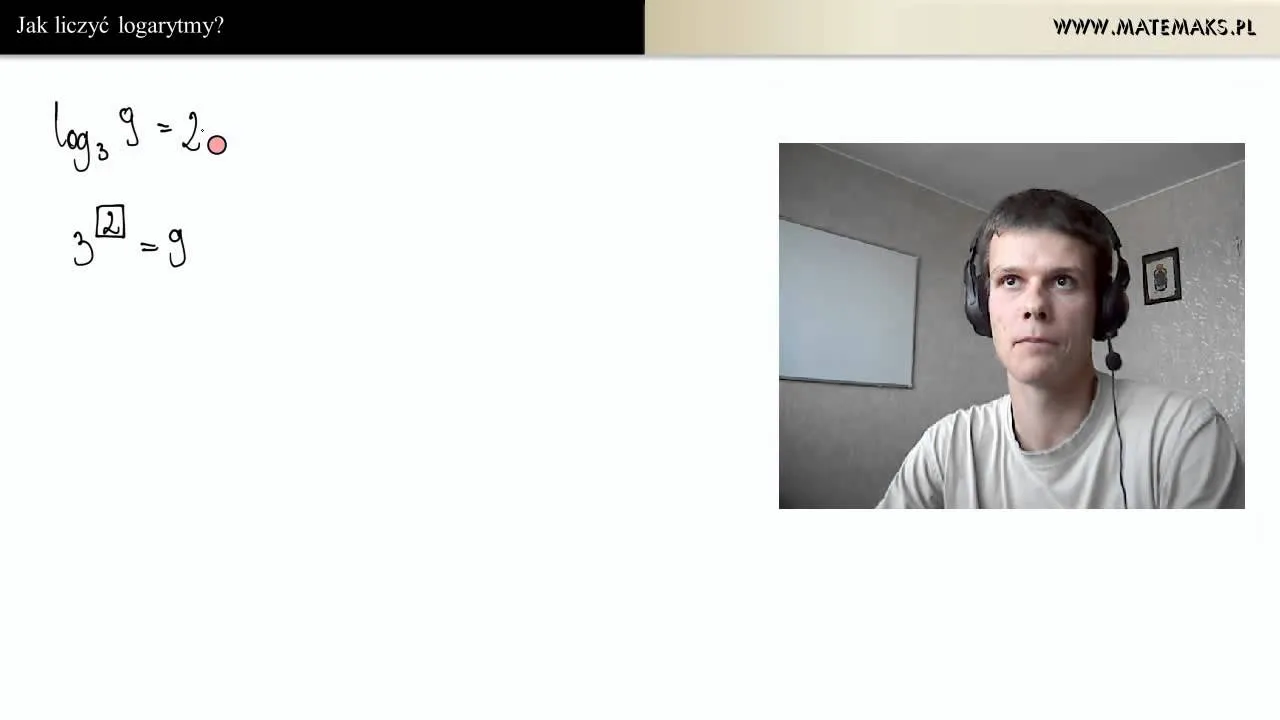
Logarytmy znajdują zastosowanie w wielu dziedzinach, a ich obliczenia są niezwykle przydatne w różnych kontekstach. W finansach, logarytmy są używane do analizy wzrostu inwestycji oraz obliczeń związanych z oprocentowaniem. Na przykład, inwestorzy często korzystają z logarytmów do określenia, jak długo zajmie im podwojenie kapitału przy danym oprocentowaniu. Dzięki tym obliczeniom, można łatwo ocenić, jakie decyzje inwestycyjne przyniosą najlepsze rezultaty.
W naukach przyrodniczych logarytmy są również kluczowe. Służą do modelowania zjawisk takich jak rozpad radioaktywny, gdzie czas półtrwania substancji można obliczyć przy użyciu logarytmów. Ważne jest, aby zrozumieć, jak logarytmy pomagają w interpretacji danych i analizie trendów, co jest niezbędne w badaniach naukowych.
Logarytmy w zastosowaniach finansowych: praktyczne przykłady
W finansach logarytmy odgrywają kluczową rolę w obliczeniach dotyczących wzrostu kapitału oraz analizy ryzyka. Na przykład, przy obliczaniu stopy zwrotu z inwestycji, inwestorzy często używają logarytmu naturalnego do oceny, jak zmienia się wartość inwestycji w czasie. Dzięki temu, mogą lepiej zrozumieć, jakie czynniki wpływają na wzrost lub spadek wartości aktywów.
| Rodzaj inwestycji | Stopa zwrotu (%) |
|---|---|
| Akcje | 8.5 |
| Obligacje | 3.2 |
| Nieruchomości | 5.0 |
Zastosowanie logarytmów w naukach przyrodniczych i technologii
Logarytmy odgrywają istotną rolę w naukach przyrodniczych i technologii, gdzie są używane do analizy i modelowania różnych zjawisk. Na przykład, logarytmy są wykorzystywane w chemii do obliczeń związanych z pH roztworów, co jest kluczowe dla zrozumienia kwasowości i zasadowości substancji. W biologii, logarytmy pomagają w modelowaniu wzrostu populacji, a w fizyce są stosowane w analizie dźwięku i jego intensywności.
Przykładem zastosowania logarytmów w naukach przyrodniczych jest skala Richtera, która mierzy magnitudę trzęsień ziemi. Ta skala jest logarytmiczna, co oznacza, że każde zwiększenie o 1 w skali Richtera odpowiada dziesięciokrotnemu wzrostowi amplitudy fal sejsmicznych. Dzięki temu naukowcy mogą lepiej ocenić siłę trzęsień ziemi i ich potencjalne skutki.
- Skala Richtera do pomiaru magnitudy trzęsień ziemi.
- Obliczenia pH w chemii, które opierają się na logarytmach.
- Modelowanie wzrostu populacji w biologii, wykorzystujące logarytmy do analizy danych.
Logarytmy w analizie danych: przyszłość i nowe możliwości
Wraz z rosnącą ilością danych generowanych w różnych dziedzinach, logarytmy stają się kluczowym narzędziem w analizie danych. W szczególności, techniki takie jak analiza regresji czy modelowanie statystyczne często korzystają z logarytmów, aby przekształcić nieliniowe związki w liniowe, co ułatwia interpretację wyników. Dzięki logarytmicznym przekształceniom, analitycy mogą lepiej zrozumieć złożone zależności i wzorce w danych, co jest nieocenione w takich dziedzinach jak marketing, biotechnologia czy ekonomia.
W przyszłości, zastosowanie logarytmów w sztucznej inteligencji i uczeniu maszynowym może przynieść jeszcze większe korzyści. Logarytmy mogą być wykorzystywane do optymalizacji algorytmów, co pozwoli na bardziej efektywne przetwarzanie i analizowanie dużych zbiorów danych. W miarę jak technologia rozwija się, logarytmy będą odgrywać coraz większą rolę w tworzeniu inteligentnych systemów, które potrafią przewidywać trendy i dostosowywać się do zmieniających się warunków rynkowych.




